Fraktale: Entdecke die geometrische Schönheit der Natur!

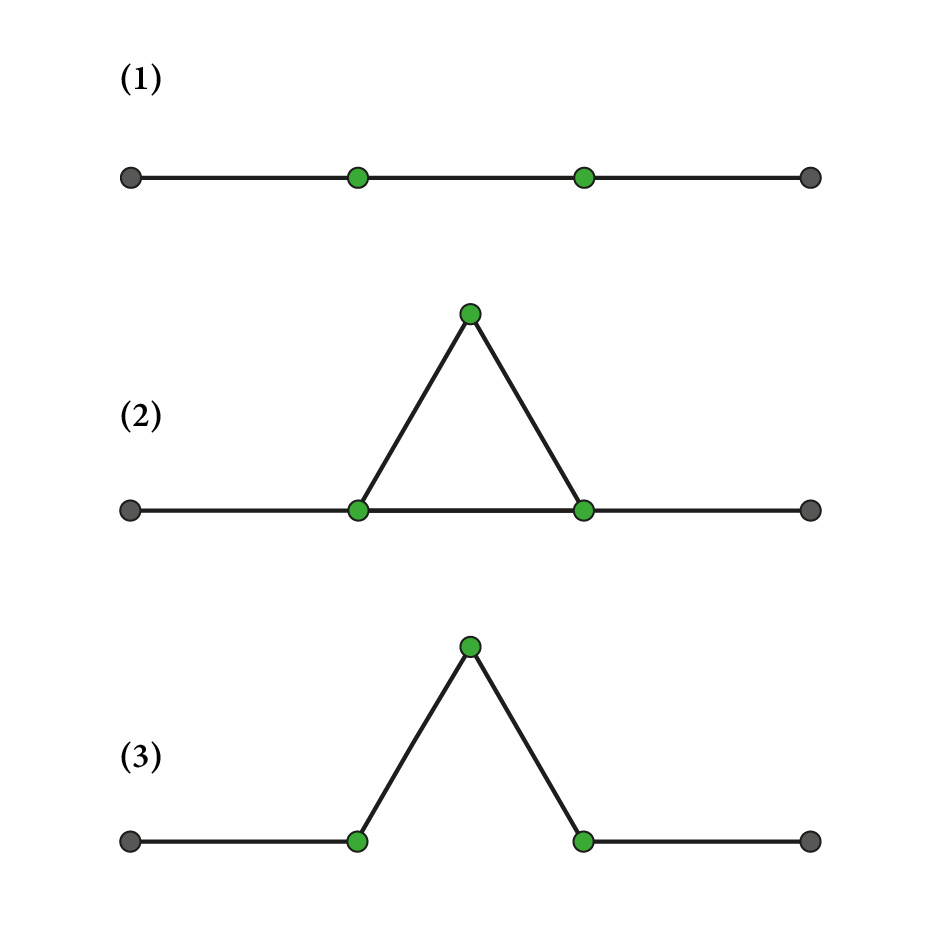
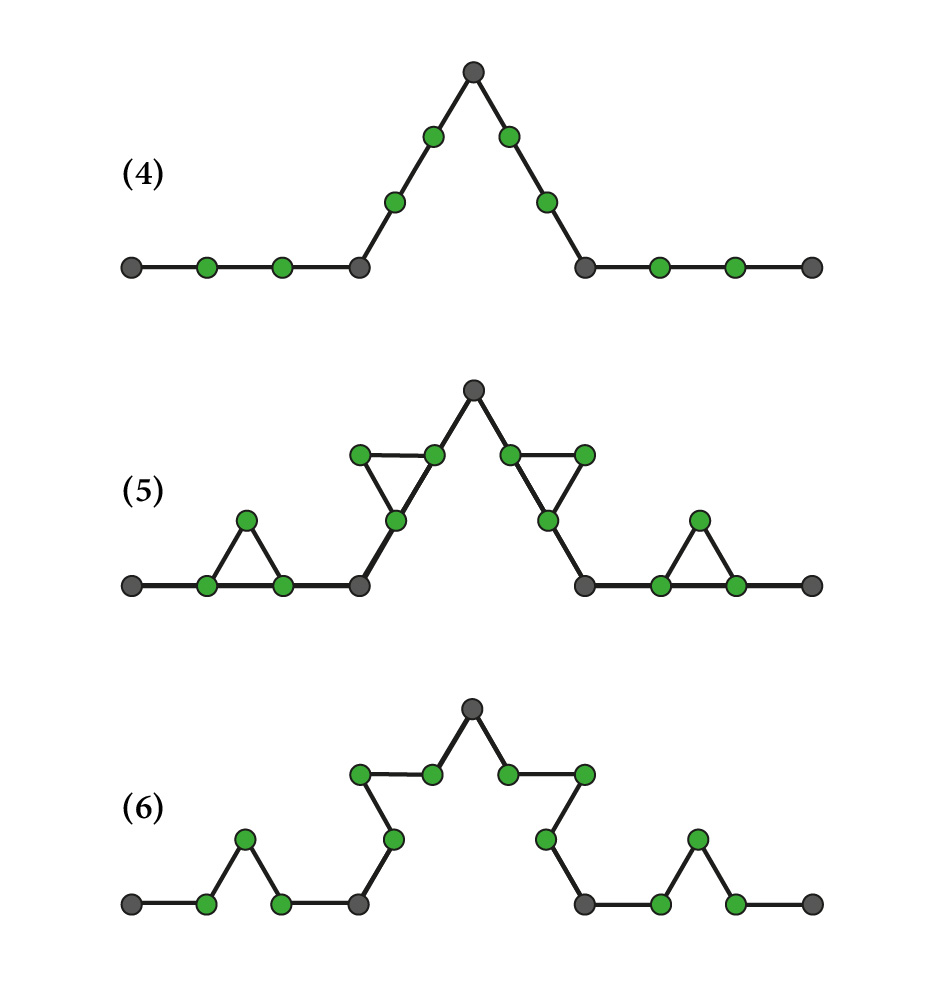
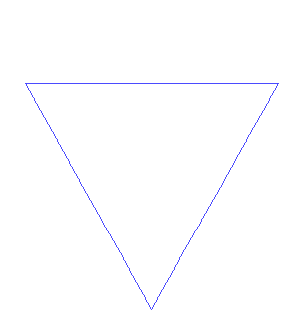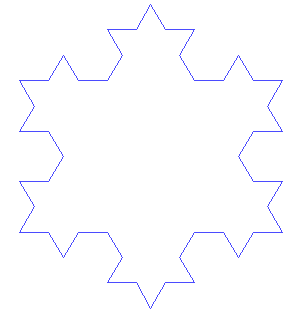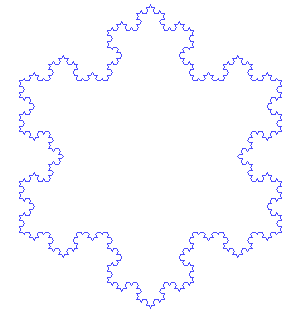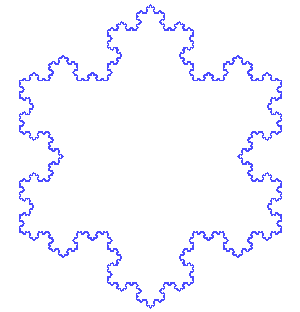
Fraktale sind geometrische Formen, die sich wiederholen, wenn man immer näher herangeht. In anderen Worten: Wenn du einen Ausschnitt aus der fraktalen Form vergrösserst, ähnelt der vergrösserte Teil der gesamten Form. Als Beispiel kannst du dir einen Tannenbaum vorstellen, von dem du einen grossen Ast heranzoomst und dabei immer kleinere Zweige erkennst, die sich wieder verzweigen und aussehen wie kleine Tannenbäume.

Romanesco-Kohl: ein essbares Fraktal!

Romanesco ist eine spezielle Blumenkohl-Züchtung. Sein „Kopf“ ist eines der schönsten Beispiele für ein natürliches, dreidimensionales Fraktal. Er besteht aus zahllosen grünen Kegeln, die an ihrer Oberfläche jeweils wieder Mini-Kegel tragen und so fort. Jedes Element ähnelt in seiner Form dem gesamten Kohlkopf.

Die Koch’sche Flocke – selbst konstruiert

Schneeflocken sind ein weiteres Beispiel für fraktale Formen, die in der Natur vorkommen. Der schwedische Mathematiker Helge von Koch beschrieb 1904 eine geometrische Form, die man heute „Koch’sche Flocke“ nennt. Du kannst sie Schritt für Schritt selbst zeichnen!

Als erstes schauen wir uns die Konstruktion der Koch’schen Kurve an:

1. Zeichne mit Bleistift eine Strecke. Teile die Strecke in drei gleich lange Abschnitte.
2. Konstruiere ein gleichseitiges Dreieck über den mittleren Abschnitt (das heisst, der mittlere Abschnitt ist die Basis des Dreiecks).
3. Radiere die Basis des Dreiecks aus.

Die Form, die du nun vor dir siehst, besteht aus vier Abschnitten. Die Schritte 1.–3. werden nun für jeden der Abschnitte wiederholt:

4. Teile jeden Abschnitt wiederum in drei gleich grosse Abschnitte.
5. Konstruiere vier gleichseitige Dreiecke, eines in der Mitte jedes Abschnitts.
6. Radiere die Basis der Dreiecke aus.

Die Koch’sche Flocke erhält man, wenn man statt von einer Strecke von einem gleichseitigen Dreieck ausgeht. Die oben beschriebene Methode wird auf jede Seite des Dreiecks angewendet und beliebig oft wiederholt – oder so lange, bis du nicht mehr kleiner zeichnen kannst …

Du wirst eine Form mit zahlreichen, immer kleiner werdenden Spitzen und Spitzchen erhalten. In jedem Ausschnitt kannst du einen Teil der Ursprungsform erkennen, mit der du begonnen hast.

Fraktale in Kunst und Wissenschaft

Kein Wunder, dass sich fraktale Computerbilder auf der Basis von solchen Algorithmen zu einer eigenen Kunstrichtung entwickelt haben! Auf der anderen Seite hat man fraktale Strukturen in immer mehr natürlichen Phänomenen entdeckt: in Wolken und Wirbelstürmen, im Verlauf von Küstenlinien oder an der Oberfläche von Geweben wie Lunge oder Darm. Die Rechenmethoden der fraktalen Geometrie helfen dabei, diese Phänomene besser zu beschreiben. Sie sind sogar in der Finanzmathematik nützlich!

Wenn du das nächste Mal am Wegrand ein Farnblatt siehst, hast du ebenfalls ein Fraktal gefunden. Erkennst du noch weitere fraktale Formen in deinem Alltag?