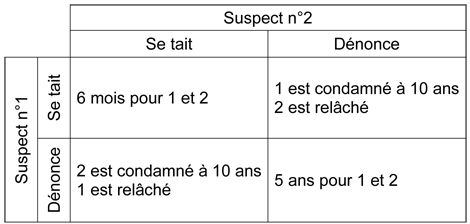
Les différentes situations envisageables et leurs conséquences pour les deux suspects. (Illustration: Rédaction SimplyScience.ch)
Deux suspects sont arrêtés par la police, et interrogés dans des salles séparées, sans moyen de communiquer. Si le premier dénonce son complice sans être dénoncé à son tour, il est relâché et son compère écope de 10 ans de prison. Si les deux individus coopèrent (dénoncent), chacun sera condamné à 5 ans de prison ; mais si les deux se taisent, ils purgeront une peine de six mois seulement. Le tableau ci-contre résume les différentes possibilités.
Une issue réellement idéale?
Remarquons que la situation est symétrique (on peut inverser 1 et 2 sans changer le tableau). L’objectif de chaque suspect est de minimiser le nombre d’années de prison. La meilleure issue possible pour un suspect donné est donc de dénoncer l’autre sans être dénoncé. En fait, il a toujours intérêt à dénoncer son complice: s’il n’est pas dénoncé en retour il sera relâché, si l’autre l’a effectivement dénoncé, il évite au moins les 10 ans de prison. La stratégie de dénonciation est dite dominante.
La situation la plus probable reste que les deux se dénoncent. C’est l’issue logique puisqu’aucun des deux ne sait ce que fait l’autre. Chaque suspect sera ainsi condamné à 5 ans de prison. S’ils s’étaient tus ils n’auraient purgé qu’une peine de six mois. En privilégiant leur intérêt individuel (minimiser leur peine pour une situation donnée), ils vont donc à l’encontre de l’intérêt collectif et sont sanctionnés pour leur égoïsme.
Il y a dilemme parce que le jeu (c’est-à-dire la situation) est à somme non nulle: la somme des années de prison de 1 et 2 n’est pas la même dans tous les cas. La dénonciation (tentante) est plus intéressante que la solidarité (les deux se taisent), mais l’égoïsme des suspects (les deux parlent) entraîne une sanction (si les deux s’étaient tus ils auraient minimisé leur peine).
Des moyens d’améliorer encore sa situation
Admettons maintenant que ce n’est pas la première fois que les deux compères se font prendre. Sachant quelle est la tendance de l’autre (coopérer et dénoncer ou être solidaire et se taire) le suspect peut adapter sa stratégie à la situation: si 2 a tendance à parler un peu trop, 1 doit impérativement le dénoncer aussi. Si au contraire 2 est muet comme une carpe, 1 a intérêt à le dénoncer afin d’être relaxé immédiatement.
Il est aussi intéressant d’intégrer d’autres contraintes au jeu: si 2 dénonce 1, alors pour se venger 1 fera assassiner la femme et les enfants de 2. Tout de suite le jeu perd sa symétrie et se déséquilibre en faveur de 1.
Un cas de base, des applications insoupçonnées
Le cas présenté dans cet article est le cas historique, tel que formulé en 1950 par Albert W. Tucker. Il caractérise en Théorie des jeux une situation où deux joueurs auraient intérêt à se montrer solidaires mais où le choix de l’intérêt personnel et de la trahison est le plus probable pour un acteur rationnel. De nombreux secteurs ont recours à ce jeu dans des variantes plus complexes: économie et finance (ex: concurrence entre deux entreprises), défense nationale (ex: choix d’une issue diplomatique ou guerrière), biologie et anthropologie (ex: cohabitation d’espèces ou de tribus, dispute des ressources du territoire). Ce jeu a donné naissance à de nombreuses théories.
Tu pourras en apprendre d’avantage sur le dilemme du prisonnier et ses variantes en lisant cet article. Pour tester tes propres stratégies, tu peux aussi visiter ce site internet plus ludique.
Alice a donc été blanchie aux yeux de l’établissement en dénonçant son camarade qui, lui, a préféré se taire. Bob s’est fait temporairement exclure. Il reste encore à Alice à s’arranger avec sa conscience et aucun rationalisme mathématique ne pourra cette fois lui venir en aide!
Texte: Rédaction SimplyScience.ch
Source: Introduction (communication orale) au cours de «logique mathématique» à l’EPFL, par le Professeur Duparc au semestre d'automne 2012.
Cet article a été automatiquement importé de notre ancien site. Merci de nous signaler, à redaction(at)simplyscience.ch, toute erreur d'affichage.