Aujourd’hui, il y a de l’information partout. Toutes les vidéos, toutes les photos, tous les articles que tu as pu lire – sont de l’information. Et comme toute information, elle doit être communiquée d’une certaine manière.
Par exemple, les êtres humains peuvent parler pour se transmettre de l’information, mais ils ont besoin d’un langage commun, comme le français ou l’allemand par exemple.
Mais quel est le langage des ordinateurs ? Comment font-ils pour se comprendre ? Heureusement, la base de leur langage leur est commune.
Il s’agit du code binaire.
Représenter les nombres...
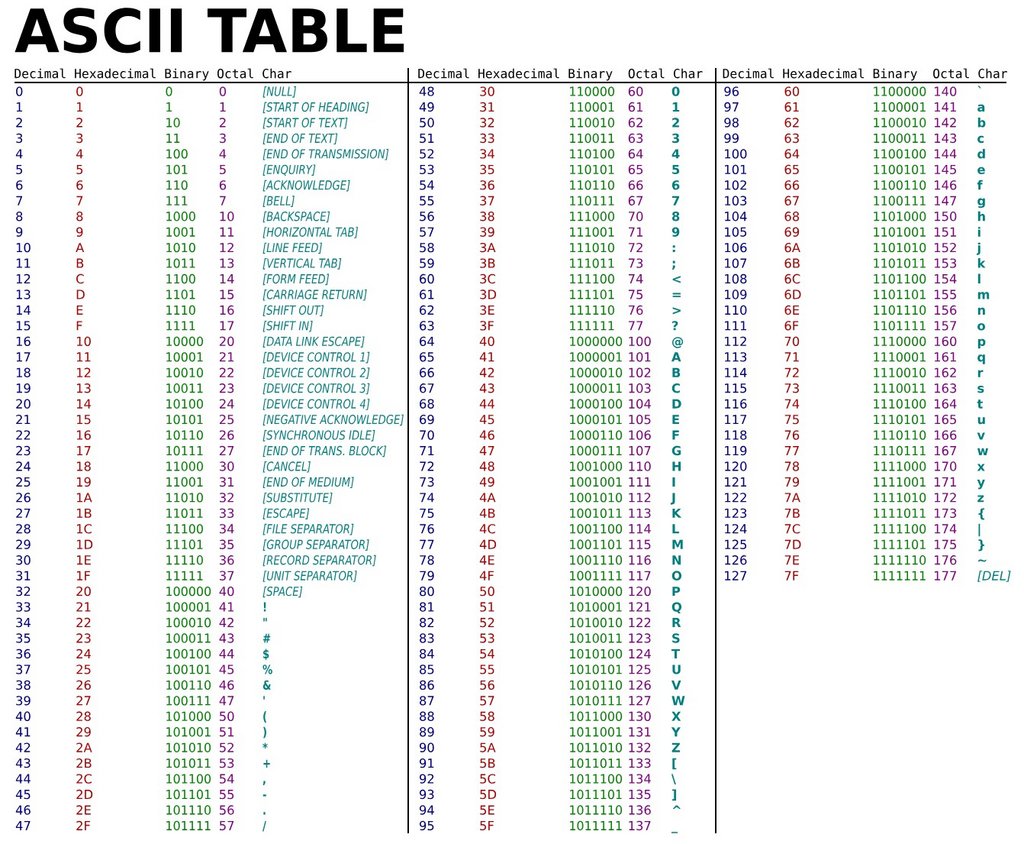
En français, il y a 26 lettres, qu’on assemble en mots et en phrases. En binaire, il n’y a que deux lettres, ou plutôt, deux chiffres – le 0 et le 1, que les ordinateurs vont utiliser pour représenter de l’information, selon des conventions communes, comme nous le faisons avec nos lettres.
Mais donc, comment peut-on écrire des mots à l’aide de 0 et de 1 ??
Avant de savoir écrire, commençons par compter. Un ordinateur a besoin de savoir représenter des nombres avant de savoir représenter des lettres. Cela deviendra bientôt plus clair.
Débutons simplement, comment écrit-on 12 en code binaire ?
La réponse est : 1100
Et maintenant 139 645 289 ?
1000010100101101000101101001
Quelle est donc cette sorcellerie ?
En fait, un ordinateur compte en base 2.
Une base, késako ?
Dans notre société, les humains comptent en base 10. C’est-à-dire qu’on utilise dix chiffres différents, de 0 à 9. Quand on arrive à 9, on utilise un 1 et un 0 pour former le 10. De manière similaire, quand on arrive à 19, on passe le 1 à 2 et le 9 à 0, pour avoir le 20. Une fois à 99, on fait apparaitre un 1, comme pour le 10, et on fait passer tous les 9 à 0, on obtient 100. En réalité, on suit un algorithme assez simple.
En partant d’un nombre, si on veut trouver le nombre suivant, on :
- Regarde le chiffre le plus à droite (1)
- Si c’est autre chose qu’un 9, on l’augmente de 1. (2)
- Sinon, on fait passer ce 9 à 0 et on regarde le chiffre à sa gauche (3)
- S’il n’y en a pas, alors on ajoute un 1 à sa gauche (4)
- S’il y en a un, alors on répète l’algorithme depuis (2) en prenant en compte ce nouveau chiffre. (5)
Ça a l’air compliqué, mais en réalité tu utilises cela lorsque tu fais des opérations simples à la main, comme des additions ou des soustractions !
Un exemple avec le nombre 1219. On veut trouver le nombre suivant - 1220.
On commence par regarder le chiffre le plus à droite (1) : c’est un 9.
On le transforme en 0. (3)
On regarde ensuite à sa gauche et on voit qu’il y a déjà plusieurs chiffres, donc on reprend l’algorithme depuis le début, avec le chiffre à sa gauche, le 1. (5)
On voit que ce n’est pas un 9, alors on l’augmente de 1, et c’est terminé. (2)
Le 9 est devenu 0 et le 1 est devenu 2 : 1219 -> 1220
Vu comme ça, c’est peut-être un peu compliqué pour quelque chose qu’on sait tous faire dans notre tête sans réfléchir… Mais patience.
...en base 2 !
Seulement, en base 2, on fait la même chose, mais on utilise seulement le 0 et le 1, en adaptant donc un peu les règles. En particulier, il n’y a pas de 9 donc le 1 jouera ce rôle puisque c’est le plus grand chiffre à notre disposition.
L’algorithme devient donc :
En partant d’un nombre, si on veut trouver le nombre suivant, on :
- Regarde le chiffre le plus à droite (1)
- Si c’est autre chose qu’un 1, on l’augmente de 1. (2)
- Sinon, on fait passer ce 1 à 0 et on regarde le chiffre à sa gauche (3)
- S’il n’y en a pas, alors on ajoute un 1 à sa gauche (4)
- S’il y en a un, alors on répète l’algorithme depuis (2) en prenant en compte ce nouveau chiffre. (5)
On commence donc tout naturellement, 0 = 0, 1 = 1. Puis, on voit qu’on n’a pas de chiffres pour représenter le 2, donc en suivant l’algorithme, on en vient à transformer le 1 en 0 et à placer un 1 devant. Ainsi, 2 = 10. En continuant à jouer avec l’algorithme, on observe que 3 = 11, 4 = 100, 5 = 101, etc.
Vérifie avec l’algorithme si tu as besoin.
Maintenant que l’on sait compter en binaire, passons à l’écriture.