Alice et Bob sont bien décidés à remporter le concours et ne veulent laisser aucune place au hasard. Ils sont persuadés que la décoration devrait tenir compte de la taille du sapin. Ils ont déjà observé qu'un sapin trop chargé de boules et de guirlandes n'est pas très beau. Mais comment faire pour le décorer juste ce qu'il faut?
Combien de décorations, de quelle forme, de quel type ?

Pour celles et ceux effrayés par ces équations, pas de panique! Un logiciel en ligne vous permet de calculer gratuitement ces valeurs.
Il faut d'abord déterminer le nombre et le type de décorations à utiliser. La question s'avère relativement complexe car tout dépend du «format» de l'arbre dont on dispose: circonférence, hauteur, «régularité»... Coup de chance! A la demande des magasins Debenhams, des étudiants en mathématiques de l'Université de Sheffield se sont penchés sur la question et ont mis au point les formules appropriées: un sapin de hauteur H cm doit être orné de (√17⁄20)*H boules, les guirlandes lumineuses doivent mesurer 13*(π/8) cm. La hauteur parfaite de l'étoile ou de la fée au sommet du conifère est évaluée à H/10 cm.
Point positif les formules présentées ci-dessus tiennent en partie compte de la «silhouette de l'arbre», malheureusement la considération n'est que partielle: pour une hauteur donnée, des sapins peuvent être plus ou moins «larges». Tout n'est pourtant pas perdu: les étudiants ont considéré le cas de sapins «standards», issus de monocultures et calibrés par des normes strictes. A moins qu'ils ne soient allés chercher un conifère en pleine forêt, les adolescents n'ont pas à se préoccuper de cette négligence.
Pour une disposition équilibrée?
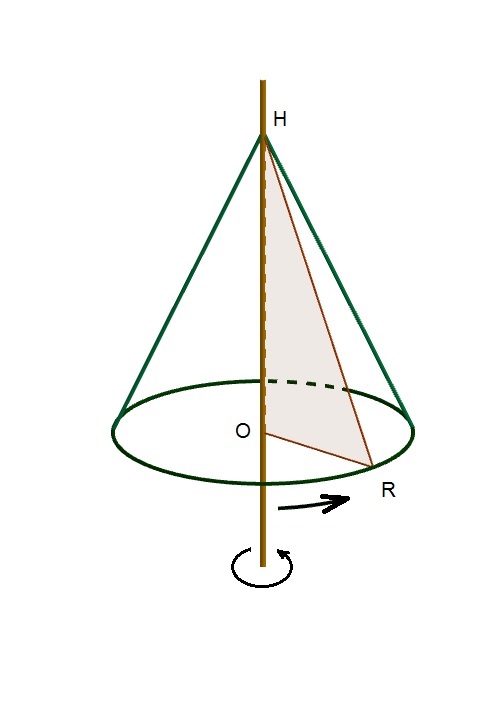
Le sapin est assimilé à un cône de révolution, le centre de gravité doit impérativement rester sur l'axe OH. (Illustration: Rédaction SimplyScience.ch)
Maintenant qu'ils savent quelles décorations utiliser et en quelle quantité, Alice et Bob doivent déterminer leur disposition. Le plus gros enjeu est d'assurer une répartition correcte des décorations afin de ne pas risquer de déséquilibrer l'arbre. Bien que sa symétrie ne soit jamais parfaite il semble raisonnable d'assimiler le sapin à un cône obtenu par révolution autour d'un axe de symétrie et reposant sur un cylindre (le tronc) qui n'est que la prolongation de cet axe.
Remarquons qu'une surcharge de l'arbre ou une perte de symétrie trop nette dans la répartition de la masse reposant sur le tronc provoquera sa chute. Ceci se justifie physiquement et mathématiquement grâce à la notion de centre de masse. Le centre de gravité d'un objet immobile est le point d'application de la force de pesanteur: il s'agit d'une grandeur physique. Il est assimilé dans notre cas (attention ce n'est pas toujours vrai) au centre de masse d'un cône de hauteur H (le tronc d'un sapin dépasse usuellement peu des branchages); en d'autres termes il s'agit ici du point du cône par rapport auquel la masse est uniformément répartie. Du fait de la symétrie supposée du sapin, ce centre de masse est situé quelque part sur le tronc (jamais en dehors, sur une branche quelconque). L'ajout de décorations va contribuer à augmenter la masse qui repose sur le tronc.
Et si tu veux vérifier, jette un œil au plus grand sapin du monde sur le flanc d'une forêt à Gubbio en Italie.
Texte: Rédaction SimplyScience.ch
Cet article a été automatiquement importé de notre ancien site. Merci de nous signaler, à redaction(at)simplyscience.ch, toute erreur d'affichage.